问题
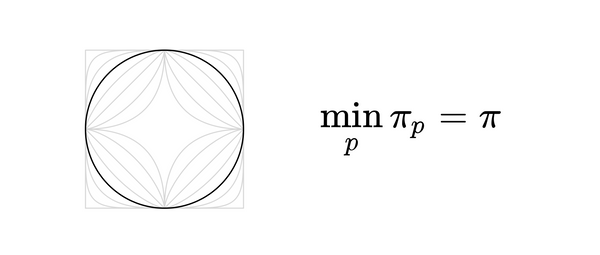
如图所示,在一个正方形的四个顶点上各有一只老鼠,每一只老鼠始终以相同速度向位于它逆时针方向相邻的老鼠移动。求:
1. 在合适的坐标系下老鼠移动轨迹的方程;
2. 老鼠移动的路程。
解法一
为了求出点的轨迹方程,以正方形的中心为极点建立极坐标系,其极轴方向平行于正方形的任意一边。设正方形的边长为$a$。我们以右上角顶点$A$处的老鼠作为研究对象。
在极坐标系中,分别设右上角顶点$A$、左上角顶点$B$的坐标为
\[A(r,\theta), B (r,\theta+\frac{\pi}{4})\]
则其对应的直角坐标分别为
\[(rcos \theta,rsin \theta)\]
与
\[(-rsin\theta,rcos\theta)\]
两点连线的斜率为
\[\begin{align}
m& =\frac{rcos\