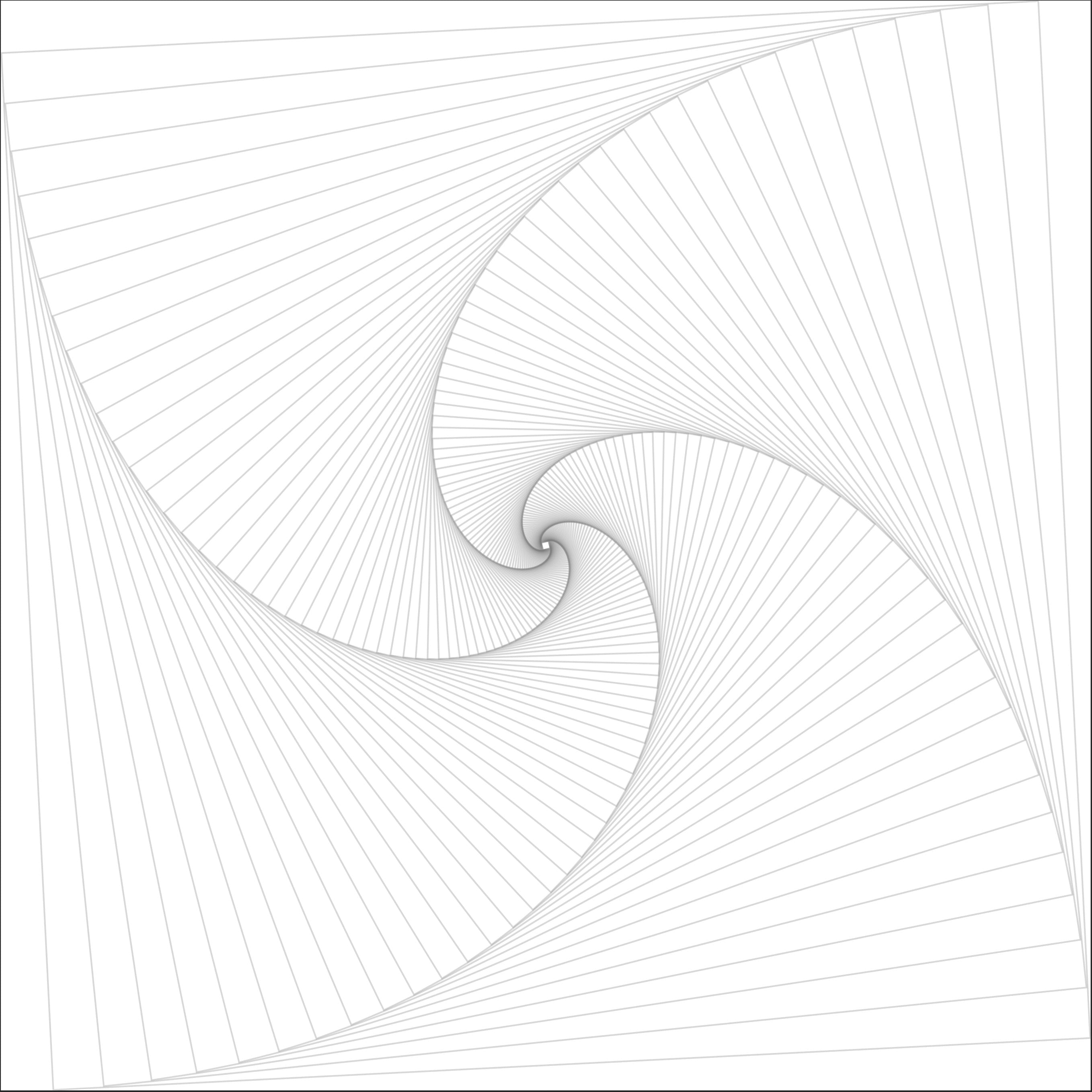
动点与对数螺线
问题

如图所示,在一个正方形的四个顶点上各有一只老鼠,每一只老鼠始终以相同速度向位于它逆时针方向相邻的老鼠移动。求:
- 在合适的坐标系下老鼠移动轨迹的方程;
- 老鼠移动的路程。
解法一
为了求出点的轨迹方程,以正方形的中心为极点建立极坐标系,其极轴方向平行于正方形的任意一边。设正方形的边长为$a$。我们以右上角顶点$A$处的老鼠作为研究对象。
在极坐标系中,分别设右上角顶点$A$、左上角顶点$B$的坐标为
\[A(r,\theta), B (r,\theta+\frac{\pi}{4})\]
则其对应的直角坐标分别为
\[(rcos \theta,rsin \theta)\]
与
\[(-rsin\theta,rcos\theta)\]
两点连线的斜率为
\[\begin{align}
m& =\frac{rcos\theta-rsin\theta}{-rsin\theta-rcos\theta}\\
& =\frac{sin\theta-cos\theta}{sin\theta+cos\theta}\\
& =\frac{tan\theta-1}{tan\theta+1}
\end{align}\]
由于A点处的老鼠的速度方向指向B点处的老鼠,因此
\[\begin{align}
m & = \frac{dy}{dx} \\
& =\frac{\frac{dr}{d\theta}sin\theta+rcos\theta}{\frac{dr}{d\theta}cos\theta-sin\theta}\\
& = \frac{\frac{dr}{d\theta}tan\theta+r}{\frac{dr}{d\theta}-rtan\theta}
\end{align}\]
为了形式上的简明,记$r'=\frac{dr}{d\theta}$,合并等式后有
\[
\frac{tan\theta-1}{tan\theta+1}=\frac{r'tan\theta+r}{r'-rtan\theta}
\]
交叉相乘后整理得
\[
r'(1+tan2\theta)=-r(1+tan2\theta)
\]
即
\[
r'=-r
\]
此微分方程有以下通解:
\[
r(\theta)=Ce^{-\theta}
\]
代入$A(\frac{\sqrt{2}}{2},\frac{\pi}{4})$得
\[
r(\frac{\pi}{4})=\frac{1}{2}\sqrt{2}a
\]
解得
\[
C=\frac{\sqrt{2}}{2}ae^{\pi/4}
\]
所以A点处老鼠在极坐标下的轨迹方程为:
\[
r(\theta)=\frac{a\sqrt{2}}{2}e^{\pi/4-\theta}
\]
这是一条对数螺线。
同理可得A、B、C、D的轨迹方程分别为:
\[
r(\theta)=\frac{a\sqrt{2}}{2}e^{\alpha-\theta},\\
\alpha=\frac{\pi}{4},\frac{3\pi}{4},\frac{5\pi}{4},\frac{7\pi}{4}
\]
老鼠移动的距离$L$可用极坐标下的弧长积分求解。由于图形的旋转对称性,四只老鼠移动的路程相等,此处以A点处的老鼠为例:
\[\begin{align}
L & = \int_{\pi/4}^{ + \infty } {\sqrt{r2+(\frac{dr}{d\theta})2}d\theta} \\
& = \int_{\pi/4}^{ + \infty } {\sqrt{a2e{\pi/2-2\theta}}d\theta} \\
& = \int_{\pi/4}^{ + \infty } {ae^{\pi/4-\theta}d\theta} \\
& = -a \cdot e{\pi/4-\theta}|_{\pi/4}{+\infty}\\
& = -a(0-1)\\
& = a
\end{align}\]
在上面的第一次变形中,用到了以下已知等式:
\[
(\frac{dr}{d\theta})2=(-r)2=r2=\frac{a2}{2}e^{\pi/2-2\theta}
\]
即老鼠移动的路程恰好等于正方形的边长。
这是我认为最漂亮严谨的一种解法。该解法来自UC Berkeley的课程《Math 53》中一道课后习题的解答,基本按照原文翻译,部分有改动,添加了一些细节。
(并不十分严谨的)解法二####
显然,直接尝试画出老鼠移动的轨迹不现实——它的速度方向随时都在变化,这也是为什么上面的常规解法需要用到微积分来处理轨迹方程。
为了简化过程,我们考虑这个连续过程的离散近似情况:在老鼠运动的总时间$t_0$中,老鼠每过一小段时间$\frac{t_0}{n}(n>0)$才改变一次方向。当$n\rightarrow \infty$时,就是题目中的实际情况。

$n=100$ 时的过程。
考虑到$\theta$不随$t$线性变化,我们换一种设法:在运动过程中,$\theta$每改变一个小角度$\theta_0=\frac{2\pi}{n}$,老鼠才改变一次方向。同样,当$n\rightarrow \infty$时,就是题目中的实际情况。
下面以$n=16$的情况作图。以极点为起点,$\frac{2\pi}{n}$为间隔,作$n$条射线,交运动轨迹于无数个点$P_i,i=1,2,...$。

留意到,由于图形的旋转对称性,因此老鼠每次运动方向的角度改变量$\alpha$是不变的,且$\alpha=\theta_0$,如图所示。
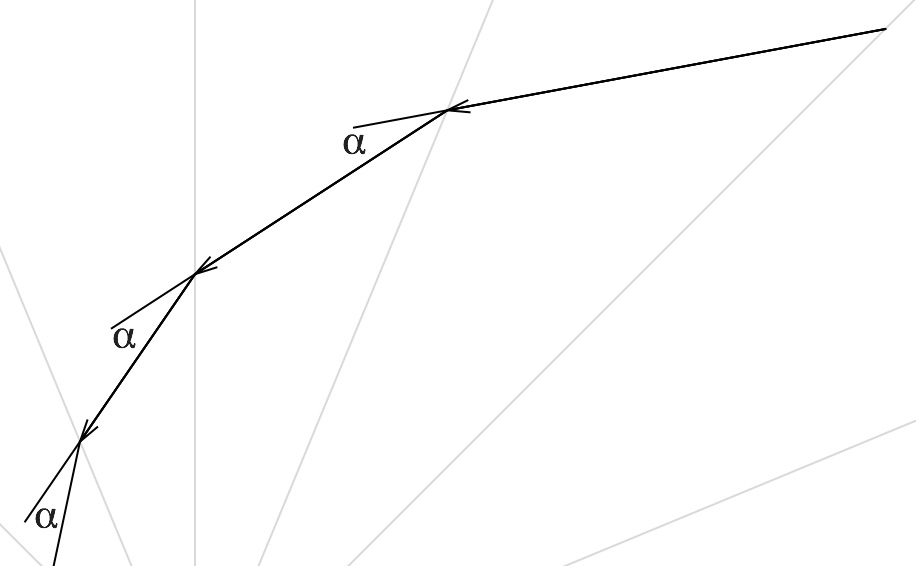
接下来证明这些点恰位于唯一的同一条对数螺线上。
引理1 对于一条对数螺线$C$上的任意一点$P$,P点与极点的连线$OP$的方向和过P点切线的夹角恒定。
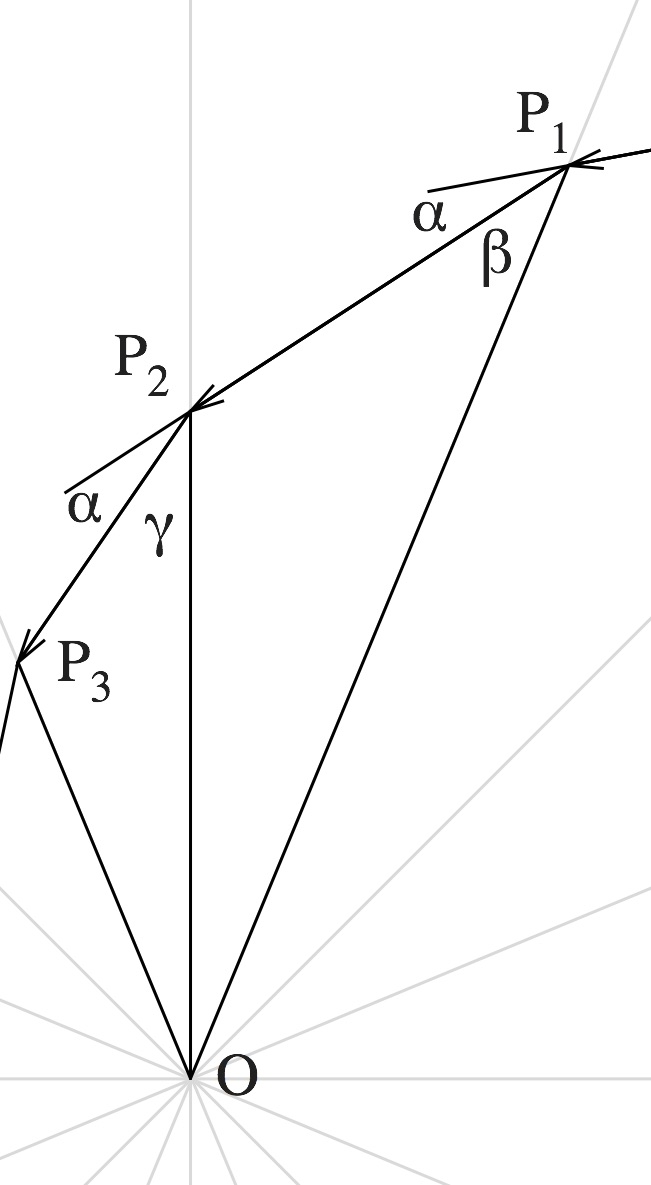
在图中,$\angle P_1OP_2=\angle P_2OP_3=\alpha$,在$\triangle P_1OP_2$中,
\[
\alpha+\gamma=\alpha+\beta
\]
当$n\rightarrow \infty$时,$\overrightarrow{P_1 P_2}$就是老鼠在$P_2$点处的速度方向,即轨迹曲线在此处的切线方向。由上面的等式可以得知,对于老鼠运动轨迹上的任意一点$P$,P点与极点的连线$OP$的方向和过P点切线的夹角恒定。
结论1 老鼠运动的轨迹是一条对数螺线。
接下来求对数螺线的方程。
引理2 对于方程为$r=ae^{b\theta}$的对数螺线,设其上的任意一点与极点的连线的方向和过该点切线的夹角为$\theta$,则$b=cot\theta$。
取正方形右上角顶点为研究对象,则$\theta=\frac{\pi}{4}$,所以$b=cot\frac{\pi}{4}=1$。
代入右上角顶点的极坐标$(\frac{\sqrt{2}}{2}a,\frac{\pi}{4})$,解得
\[
r=\frac{a\sqrt{2}}{2}e^{\pi/4-\theta}
\]
结论2 老鼠运动的轨迹方程为$r=\frac{a\sqrt{2}}{2}e^{\pi/4-\theta}$
其余四点同理。
结论
老鼠的轨迹是四条对数螺线,形成夹角为$\frac{\pi}{2}$的旋转对称,每条的长度均等于正方形的边长,它们交于正方形的中心。

然后呢
本问题中,正方形可以推广到正n边形,结论会有一些异同。
为了简化问题,可以设这些正n边形均内接于单位圆。
结论可以参见这篇MathWorld的词条。

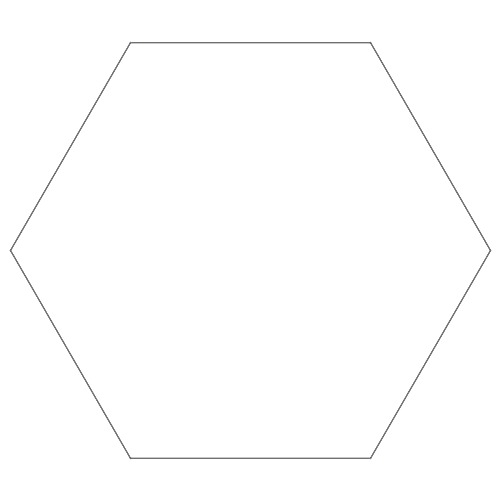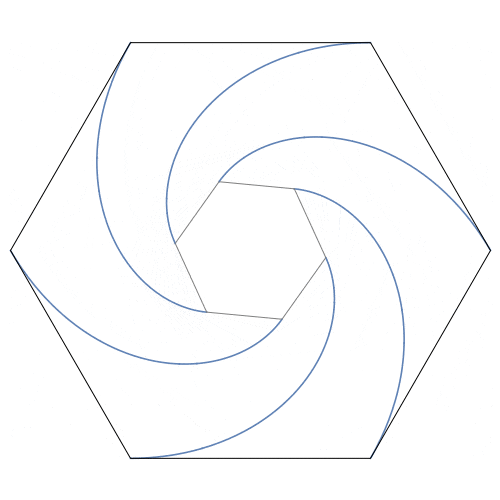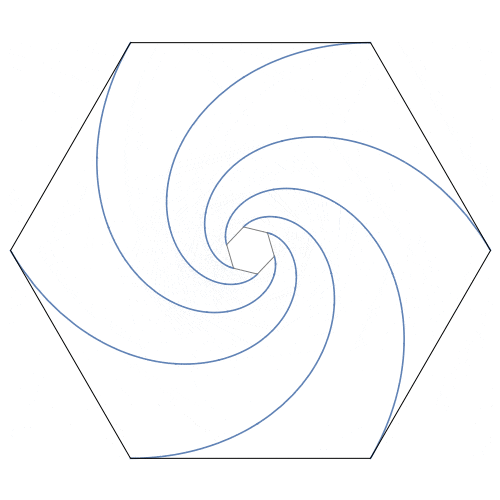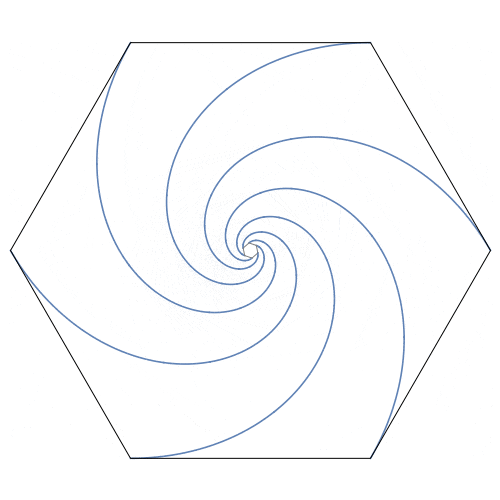
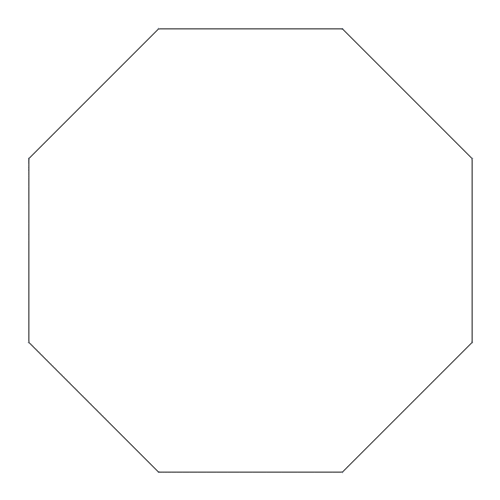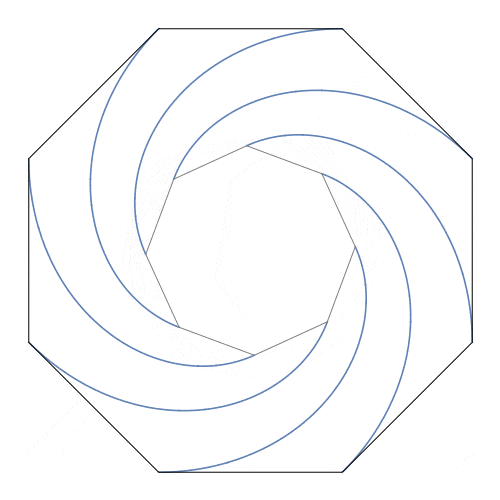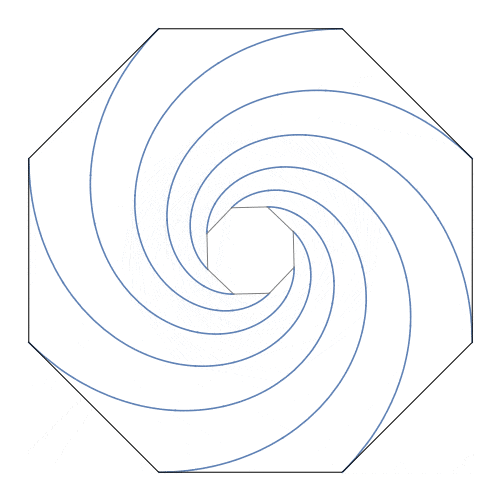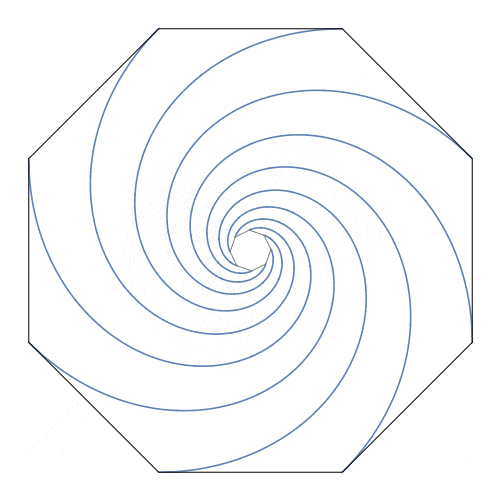
思考####
- 结论与然后呢中动图的表现方式有什么不同?结合下面的配图,你能联想到什么?
- 为什么任意中心位于原点的对数螺线的方程都能用$r=ae^{b\theta}$来表示?能不能在别的位置添加新的参数?
- 当四只老鼠的速度不相同时,轨迹形状会发生怎样的变化?尝试画出大致图形。
- 解法二与解法一相比,无需使用较为高深的微积分,但同时也没有给出第二小问的解。你能不用微积分解出第二小问吗?