π是圆周率的最小值
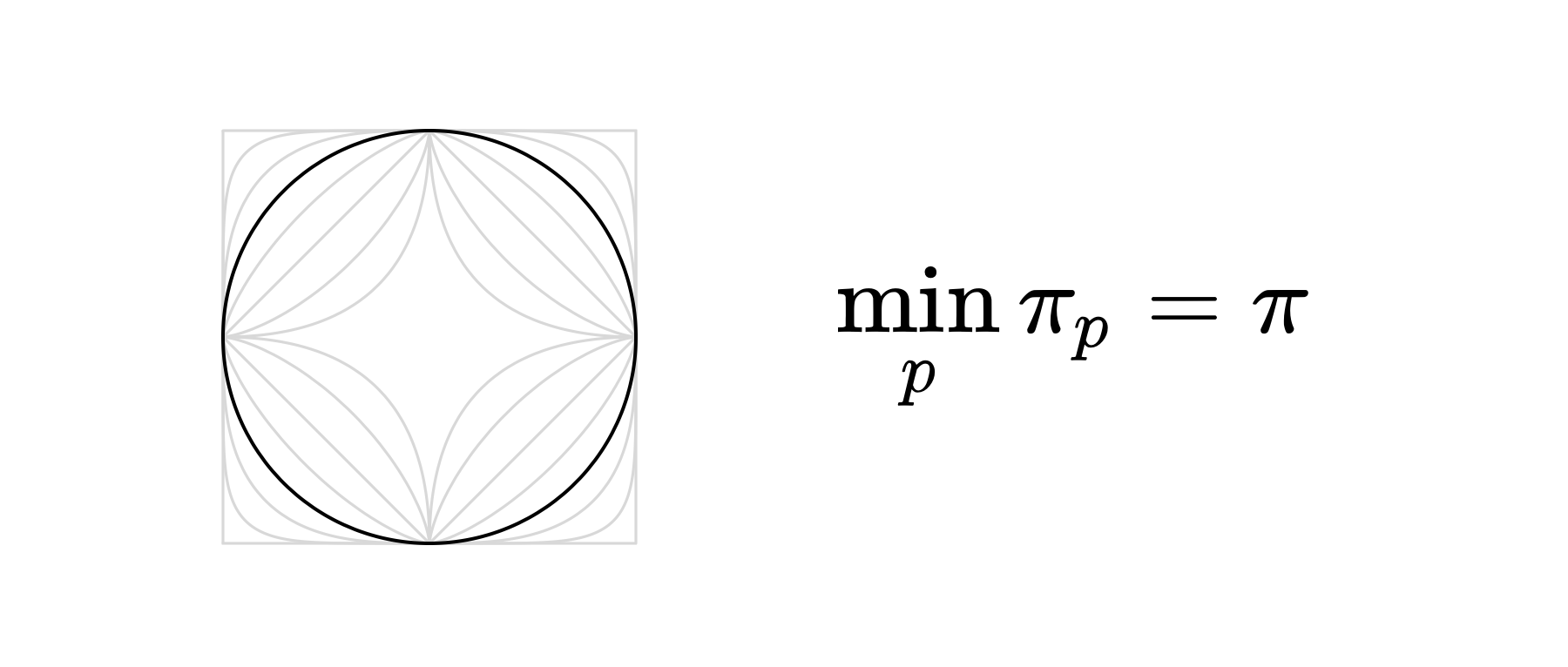
我们都知道$\pi=3.14159265359\dots$是圆的周长与其直径的比值。但如果改变“长度”的定义,圆周率还会保持不变吗?
当长度不再是长度
在二维欧氏空间$\mathbb{R}^n$中,向量$\vec{x}=(x_1,x_2,\dots,x_n)$的长度为
$$
| \vec{x} | = \sqrt{x_1^2+x_2^2+\cdots+x_n^2} = (\sum_{i=1}^n x_i^2)^\frac{1}{2}
$$
这是由勾股定理得出的。
然而,对于一个抽象的向量空间$V$而言,其不一定具有“长度”的概念。为了将长度推广到其他的向量空间上,我们可以将长度抽象为拥有一些长度所具备的性质的函数,称为范数(norm)。在本文中,为了将范数与绝对值区别开来,采用双竖线(如$\Vert \vec x \Vert$)表示范数。
域$F$上的向量空间$V$中的范数$\Vert \cdot \Vert: V \to \mathbb{R}$必须满足以下三个条件:
对于任意的$\vec{u},\vec{v} \in V, a \in F$,
- $\Vert \vec u \Vert \geq 0$且$\Vert \vec u \Vert = 0 \iff \vec u = \vec 0$(半正定性)
- $\Vert a \vec u\Vert = |a|\Vert \vec u \Vert$(绝对齐次性)
- $\Vert \vec u + \vec v \Vert \leq \Vert \vec u \Vert + \Vert \vec v \Vert$(三角不等式)
可以验证一开始提到的“长度函数”是$\mathbb{R}^n$上的范数。在$\mathbb{R}^n$中,根据形式将其定义推广,从而得到一类范数,称为$p$-范数或$\ell_p$-范数:
$$
\Vert \vec x \Vert_p = (\sum_{i=1}^{n} |x_i|^p)^{\frac{1}{p}}
$$
需要注意的是,当$p \geq 1$时,$\Vert \cdot \Vert _p$的确是$\mathbb{R}^n$中的范数。但当$0<p<1$时,$\Vert \cdot \Vert _p$不满足三角不等式,因而不是范数。
相应地,我们也可以同样将距离的概念推广,称为度量(metric)。“距离”也就是两个向量之差的“长度”,因此自然地,我们可以这样定义$p$-范数下的距离:
$$
D_p(\vec x, \vec y) = \Vert \vec x - \vec y \Vert_p = (\sum_{i=1}^{n} |x_i-y_i|^p)^{\frac{1}{p}}
$$
这一由$p$-范数诱导的度量有一个特殊的名字,称为Minkowski距离。具备这一度量的几何称为Minkowski几何(此处指的不是广义相对论里的Minkowski几何)。
类似地,度量也需要满足一些条件。但由于用这种方式通过范数定义的函数一定是度量,此处略去具体条件。
当圆不再是圆
为了简便,本章中只讨论$\mathbb{R}^2$中的情况。
回想一下,单位圆(unit circle)的定义是到原点距离为1的点的集合,即范数为1的点的集合。设$C_p$为$p$-范数意义下的单位圆,则
$$
C_p = { (x,y) \in \mathbb{R}^2:|x|^p+|y|^p=1 }
$$
同样,定义$B_p$为$p$-范数意义下的单位球,即$C_p$所围成的区域:
$$
B_p = { (x,y) \in \mathbb{R}^2:|x|^p+|y|^p \leq 1 }
$$
以下是$p$取不同值时的$C_p$:

当$p \to \infty$时,$C_p$逐渐趋向于一个四边平行于坐标轴的正方形,即${ (x,y) \in \mathbb{R}^2 : \max(x,y) = 1 }$。根据这一现象,定义
$$
\Vert \vec x \Vert_\infty=\max_{1 \leq i \leq n} |x_i|
$$
事实上,可以直接证明(参见附录)
$$
\Vert \vec x \Vert_\infty = \lim_{p\to\infty} \Vert \vec x \Vert_p
$$
还可以发现$0<p<1$时单位圆所围的图形是凹的,这恰恰说明对应的$\Vert \cdot \Vert_p$不是范数。假设$\Vert \cdot \Vert_p$是范数,则单位圆所围的图形必定是凸的。
当$p=1$时,对应的Minkowski距离为横竖坐标的差的绝对值之和,即
$$
D_1(\vec x, \vec y) = |x_1-y_1| + |x_2-y_2|
$$
称为曼哈顿距离,来源于曼哈顿整齐的长方形街区布局。也可以想象成方格棋盘上一个只能往上、下、左、右四个方向移动的棋子从一点移动到另外一点所需要的距离。
当$p=2$时,就回到了最熟悉的欧几里得距离:
$$
D_2(\vec x, \vec y) = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2}
$$
当$p\to\infty$时,对应的Minkowski距离则是横竖坐标的差的绝对值的最大值,也就是
$$
D_\infty(\vec x,\vec y) = \max_{1 \leq i \leq n}|p_i-q_i|
$$
称为Chebyshev距离。国际象棋中的王既可以横竖走一步,又可以沿对角线走一步,因此Chebyshev距离可以看成是王从一点移动到另外一点所需要的距离。
圆周率还是π吗?
回忆一下,圆周率的定义是圆的周长与直径之比。当$p$改变时,单位圆也在变化,那么圆周率也会改变吗?
考虑$p$改变后,可能会影响圆周率的因素:
- 单位圆的直径不变,均为2
- 距离的定义发生了变化,导致弧长的计算公式也产生了变化
看来圆周率也会变化。接下来我们用积分计算一下周长,然后就可以算出圆周率了。
设$\pi_p$为p-范数意义下的圆周率。
根据对称性,我们只需要计算第一象限内的弧长然后乘以4就可以了。考虑第一象限内圆弧的参数方程
$$
\begin{cases}
x=u^{1/p} \\
y=(1-u)^{1/p}
\end{cases}
\quad u\in[0,1]
$$
弧长微元
$$
\begin{align*}
\mathrm{d}s &= (\left| \frac{\mathrm{d}x}{\mathrm{d}u} \right|^p + \left| \frac{\mathrm{d}y}{\mathrm{d}u} \right|^p)^\frac{1}{p} \mathrm{d}u \\
&= \frac{1}{p} (u^{1-p}+(1-u)^{1-p})^\frac{1}{p} \mathrm{d}u
\end{align*}
$$
单位圆的直径为2,因此圆周率为
$$
\begin{align*}
\pi_p &= \frac{4 \int_0^1 \frac{1}{p} (u^{1-p}+(1-u)^{1-p})^{1/p} \mathrm{d}u}{2} \\
&= \frac{2}{p} \int_0^1 (u^{1-p}+(1-u)^{1-p})^{1/p} \mathrm{d}u \\
&= \frac{2}{p} \int_0^1 \frac{(u^{p-1}+(1-u)^{p-1})^{1/p}}{(u(1-u))^{(p-1)/p}} \mathrm{d}u
\end{align*}
$$
遗憾的是,对于大多数的$p$,这个积分没有解析解,除了这几个:$\pi_1=4,\pi_2=\pi,\pi_\infty=4$。
而对于其他的$p$,利用数值积分的方法, 可以计算出$\pi_p$的近似值:
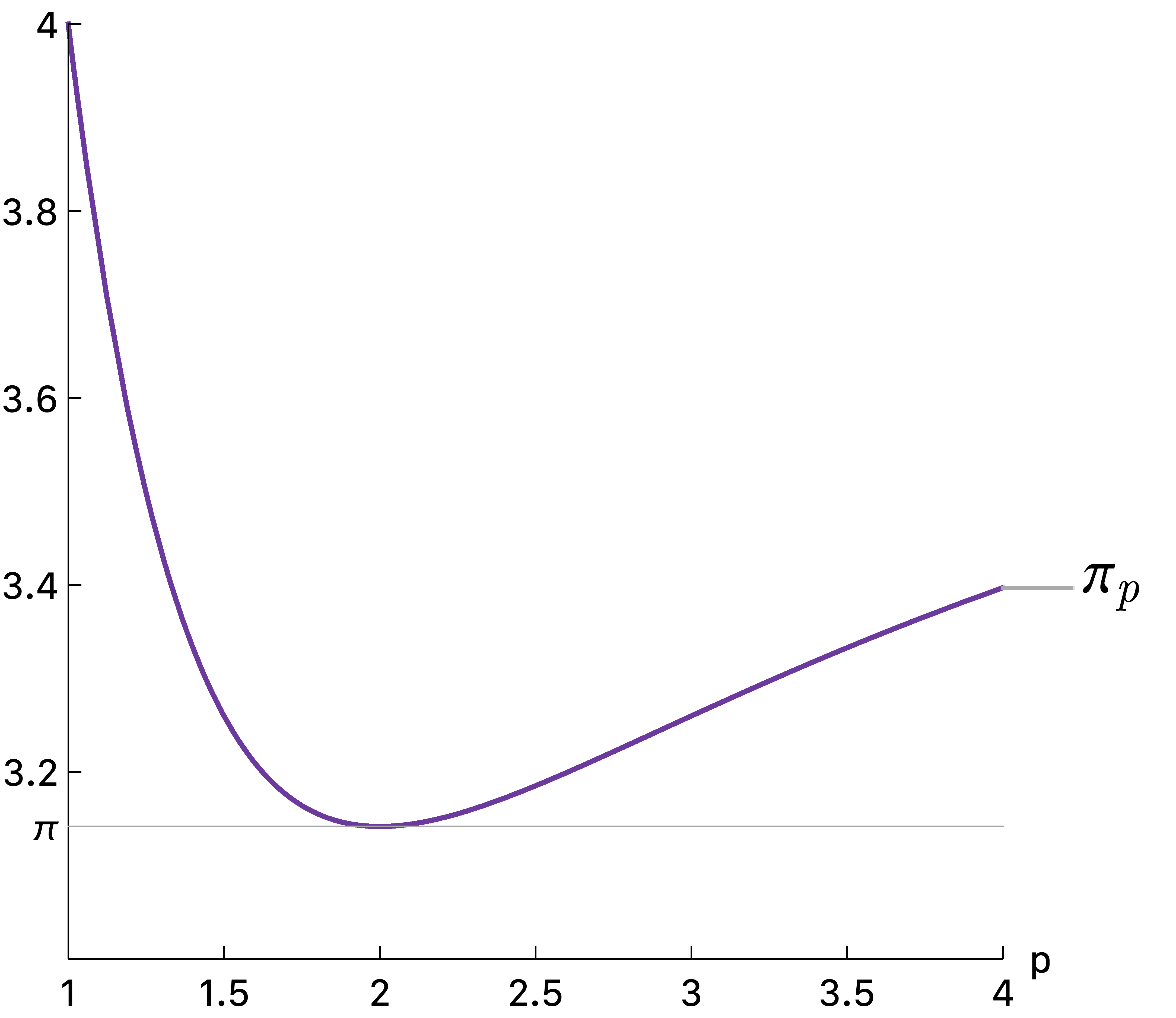
从图中能看出两点:
$\pi_p \in [\pi, 4] \quad \forall p\geq 1$
当$p=2$时,$\pi_p$取得最小值$\pi$
为了证明这两点,在[1]中,作者提出了一个$\pi_p$的下界,称为$\Pi_p$:
$$
\begin{align*}
\Pi_p &= \frac{2}{p} \int_0^1 \frac{u^{2(p-1)/p}+(1-u)^{2(p-1)/p}}{(u(1-u))^{(p-1)/p}} \mathrm{d}u \\
&= \frac{4}{p} \int_0^1 u^{(p-1)/p}(1-u)^{-((p-1)/p)} \mathrm{d}u
\end{align*}
$$
利用Beta函数的定义,可以得到
$$
\Pi_p = 4\Gamma(1+\frac{1}{p})\Gamma(2-\frac{1}{p})
$$
并可以进一步证明以下引理:
$\Pi_p \leq \pi_p \quad \forall p\geq 1$
$\Pi_1 = 4 = \pi_1$
$\Pi_2 = \pi = \pi_2$
$\Pi_\infty = \lim_{p\to\infty} \Pi_p = 4 = \pi_\infty$
当$p=2$时,$\Pi_p$取得最小值
由此便可推出$p=2$时,$\pi_p$也取得最小值。之前从图中观察到的两点得证。下图为$\pi_p$与$\Pi_p$关于$p$的曲线:
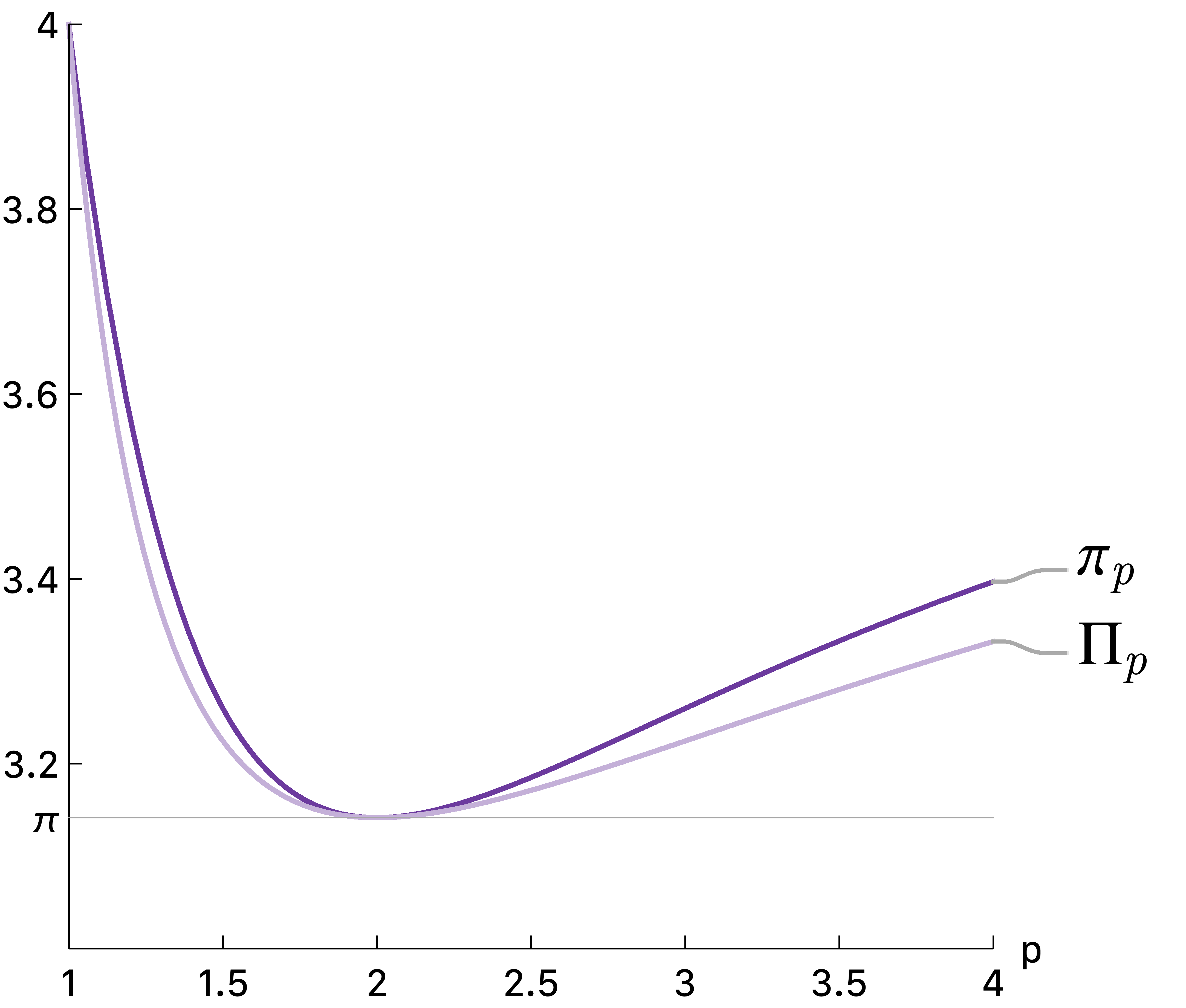
具体的推导过程详见[1]。
因此,可以说$\pi$是$p$-范数意义下圆周率的最小值。
除此之外,从图中还可以大致看出$\frac{1}{p} + \frac{1}{q}=1 \implies \pi_p = \pi_q$,而这个形式和Hölder不等式的条件完全相同。在[2]中,作者除了给出一种通过对积分进行变形的证明方法外,还提到了另一种几何的角度的证明。留意到$B_p$和$B_q$互为极集(polar set),即
$$
B_p = { \vec x\in \mathbb{R}^2: \vec x \cdot \vec y \leq 1, \vec y \in B_q }
$$
根据[3]的结论即可得到结论。
方圆之间
2012年10月,曾负责iOS界面设计的Scott Forstall从Apple离职。
2013年6月,由Jony Ive领导设计的iOS 7发布。其中很难注意到的是,iOS app图标的形状第一次发生了变化。
在iOS 7前,iOS app图标的形状是一个圆角矩形,四角均为四分之一圆弧。其优点在于实现简单,但同时也存在视觉上的问题:圆弧部分到直线部分的曲率过渡是不连续的。
曲线在某点处的曲率定义为该点处密切圆的半径的倒数。在圆角矩形的直线部分,曲率为0;在圆弧部分,曲率为$1/r$,其中$r$为圆弧的半径。因此,在直线与圆弧的接合点处,曲率会突然从0跳到$1/r$,或是从$1/r$跳到0,导致视觉上不够平滑。
以下是曲率$\kappa$随弧长$s$的变化:

iOS 7之后,Apple转为采用一种叫做超椭圆(superellipse)的形状:

熟悉吗?这正是$p=5$时单位圆的形状!它的曲率过渡则平滑得多:
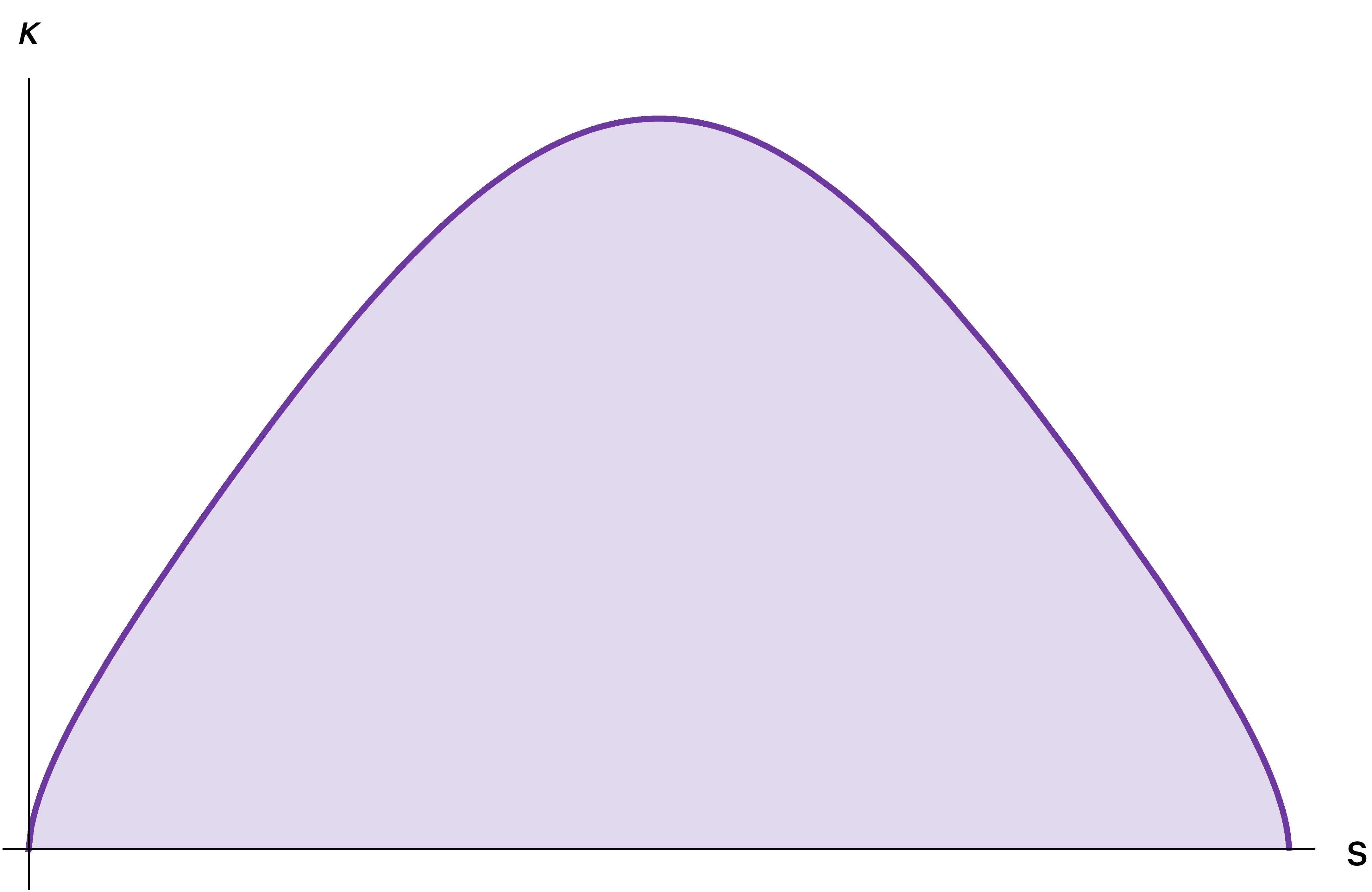
两者在形状上十分相近:

之所以叫超椭圆,则是由于其方程是由椭圆推广得来的:
$$
\left|\frac{x}{a}\right|^p+\left|\frac{y}{b}\right|^p=1
$$
工业设计中,常用G0、G1、G2、G3表示曲线连续性的不同级别:
连续量对应的几何量G0/曲线本身G1一阶导数切线G2二阶导数曲率G3三阶导数挠率
例如:正方形是G0的,因为两边的切线会在四角处突变;圆角矩形是G1的,理由上文已经提及;超椭圆由于是光滑的,自然是G3的(当然还可以更高,但没必要)。
附录
以下为
$$
\Vert \vec x \Vert_\infty = \lim_{p\to\infty} \Vert \vec x \Vert_p
$$
的证明。
若$\vec x = \vec 0$,则$\Vert \vec x \Vert_\infty = \lim_{p\to\infty} \Vert \vec x \Vert_p = 0$。下设$\vec x \neq \vec 0$。
留意到存在$1 \leq i \leq n$使得$x_i \neq 0$,因此$\Vert \vec x \Vert_\infty > 0$。
由定义,有
$$
\Vert \vec x \Vert_\infty \geq |x_i| \quad \forall \ 1\leq i \leq n
$$
于是
$$
\left( \frac{|x_i|}{\Vert \vec x \Vert_\infty} \right)^p \leq 1 \quad \forall \ 1\leq i \leq n
$$
累加不等式得
$$
\sum_{i=1}^n \left( \frac{|x_i|}{\Vert \vec x \Vert_\infty} \right)^p \leq n
$$
因此
$$
\begin{align*}
\Vert \vec x \Vert_p &= (\sum_{i=1}^{n} |x_i|^p)^{\frac{1}{p}}\
&= \Vert \vec x \Vert_\infty \frac{(\sum_{i=1}^n |x_i|^p)^\frac{1}{p}}{\Vert \vec x \Vert_\infty} \
&= \Vert \vec x \Vert_\infty \left( \sum_{i=1}^n \frac{|x_i|^p}{\Vert \vec x \Vert_\infty^p} \right)^\frac{1}{p} \
&= \Vert \vec x \Vert_\infty \left( \sum_{i=1}^n \left( \frac{x_i}{\Vert \vec x \Vert_\infty} \right)^p \right)^\frac{1}{p} \
&\leq n^\frac{1}{p} \Vert \vec x \Vert_\infty
\end{align*}
$$
另一方面,有
$$
\begin{align*}
\Vert \vec x \Vert_p &= (\sum_{i=1}^{n} |x_i|^p)^{\frac{1}{p}} \
&\geq \left( (\max_{1 \leq i \leq n} |x_i|)^p \right)^\frac{1}{p} \
&= (\Vert \vec x \Vert_\infty^p )^\frac{1}{p} \
&= \Vert \vec x \Vert_\infty
\end{align*}
$$
结合两个不等式,
$$
\Vert \vec x \Vert_\infty \leq \Vert \vec x \Vert_p \leq n^\frac{1}{p} \Vert \vec x \Vert_\infty
$$
令$p\to\infty$,得
$$
\Vert \vec x \Vert_\infty \leq \lim_{p\to\infty} \Vert \vec x \Vert_p \leq \Vert \vec x \Vert_\infty
$$
于是
$$
\Vert \vec x \Vert_\infty = \lim_{p\to\infty} \Vert \vec x \Vert_p
$$
证毕。
参考文献
[1] Adler, Charles Laurance, and James Tanton. "π is the minimum value for Pi." The College Mathematics Journal 31.2 (2000): 102-106.
[2] Keller, Joseph B., and Ravi Vakil. "π p, the Value of π in ℓp." The American Mathematical Monthly 116.10 (2009): 931-935.
[3] Schäffer, Juan Jorge. "The self-circumferences of polar convex disks." (1971).