乘法表、轮子和马克杯

在阳光或灯光下的马克杯里,常常会出现心形的亮斑。
很久以前就想探究一下这个问题,最近又看到了这个现象,于是去查了一下。
结果自然是标准结局:早就被人研究过了。
在解释这个现象之前,先来看一些看似完全无关的其他现象吧。
1 乘法表
接下来我们要制作一个环形的“乘法表”。
设$n,m$为正整数,$n$是数字的个数,$m$是乘数。这里我们取$n=12$和$m=3$。现在我们将$0$到$n-1$这$n$个整数等距依次排列在一个圆上,就像时钟一样:
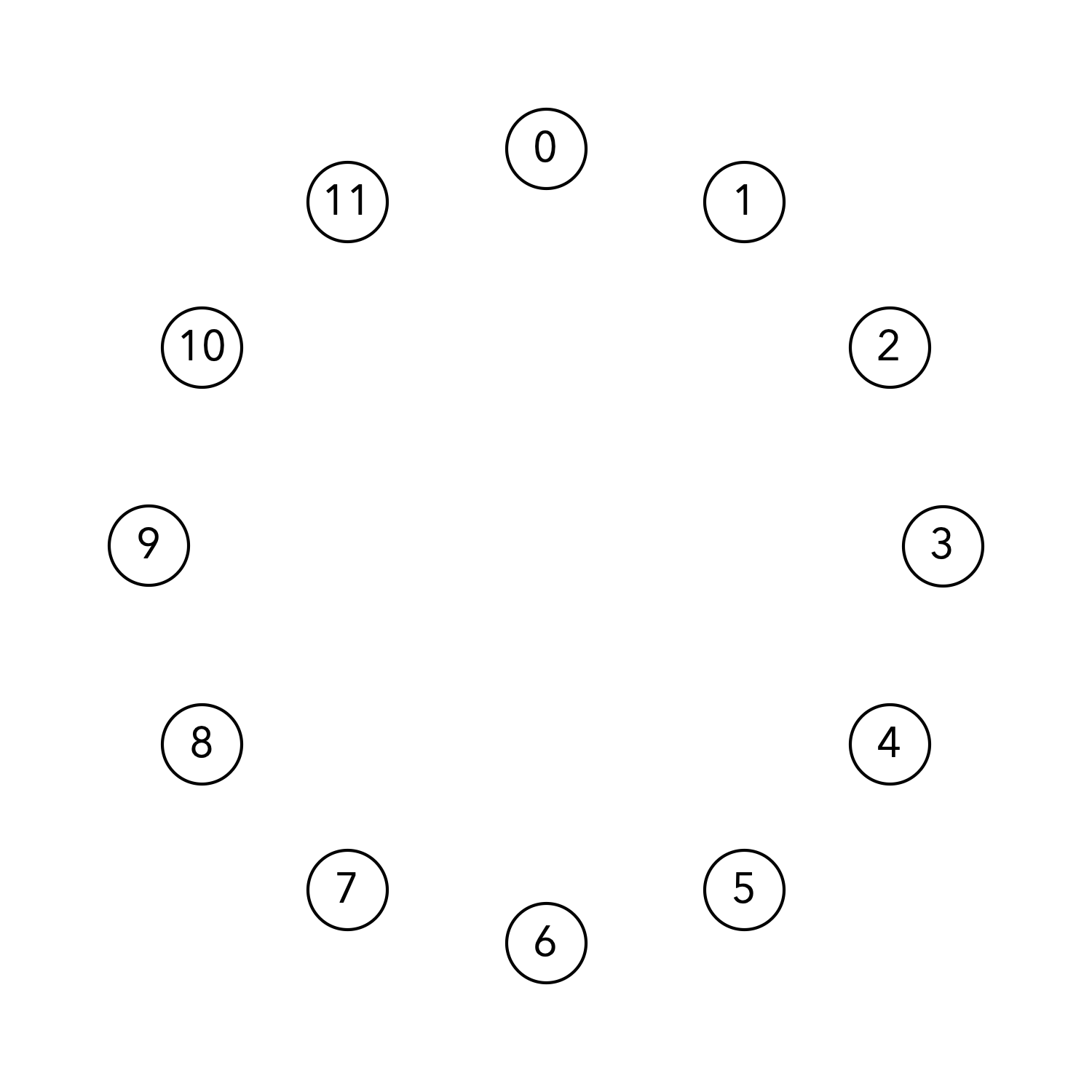
然后按照以下的规则连线:对其中任意一个数$k$,计算$r = mk \mod n$,即m与k的乘积除以n的余数,
- 如果$k=r$,则略去,不连线。
- 如果$k\neq r$,则连接$k$与$r$。
如果将每个数看成是由$0$开始沿着圆周顺时针走的步数,那么$r$和$mk$实际上是同一个位置。
例如,对于$k=10$,由于$mk=3\cdot10=30=2\cdot12+6=2n+6$,因此余数$r=6$。从$0$开始顺时针走30步,也就是绕了2圈后回到$0$,然后再走6步。所以我们把10和6连起来:
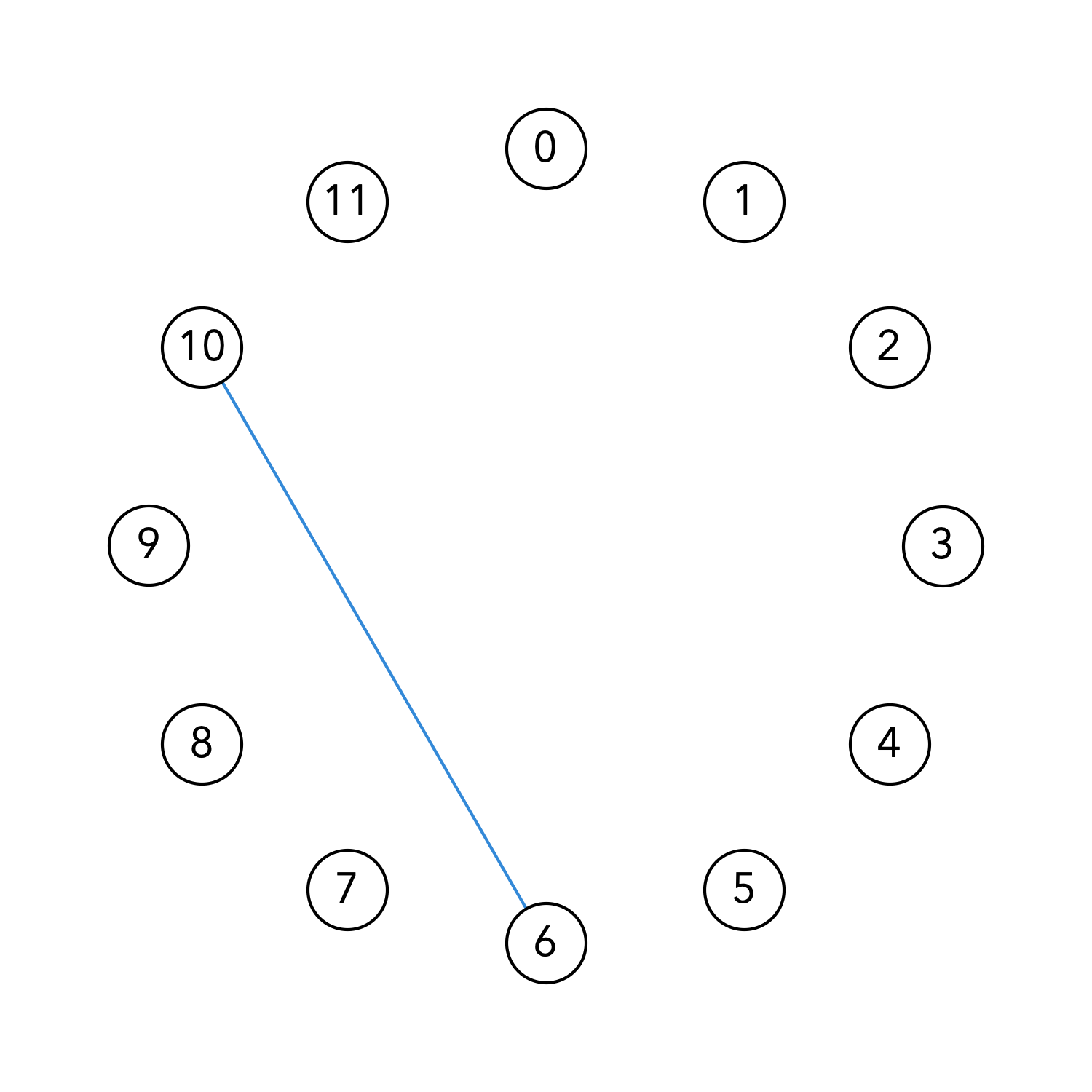
类似地,对这12个数都进行同样的操作,最终会得到这样的图:
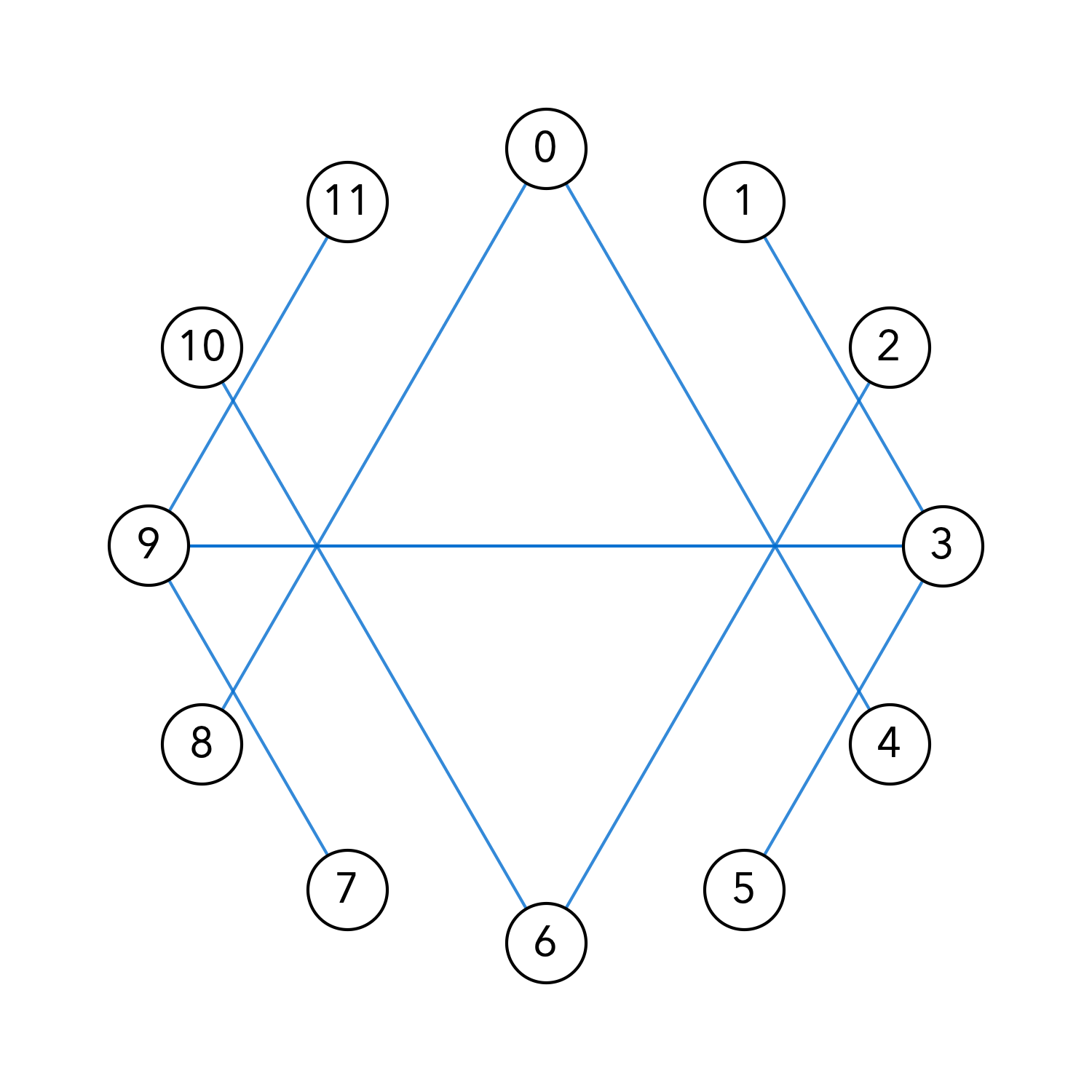
看起来似乎没有什么特别的,和一开始杯子里亮斑的形状也没有什么关系。
接下来我们固定$m=3$,然后增大$n$,即圆周上点的数量。(由于$n$会比较大,顶点就省略不画了)
当$n=100$时:
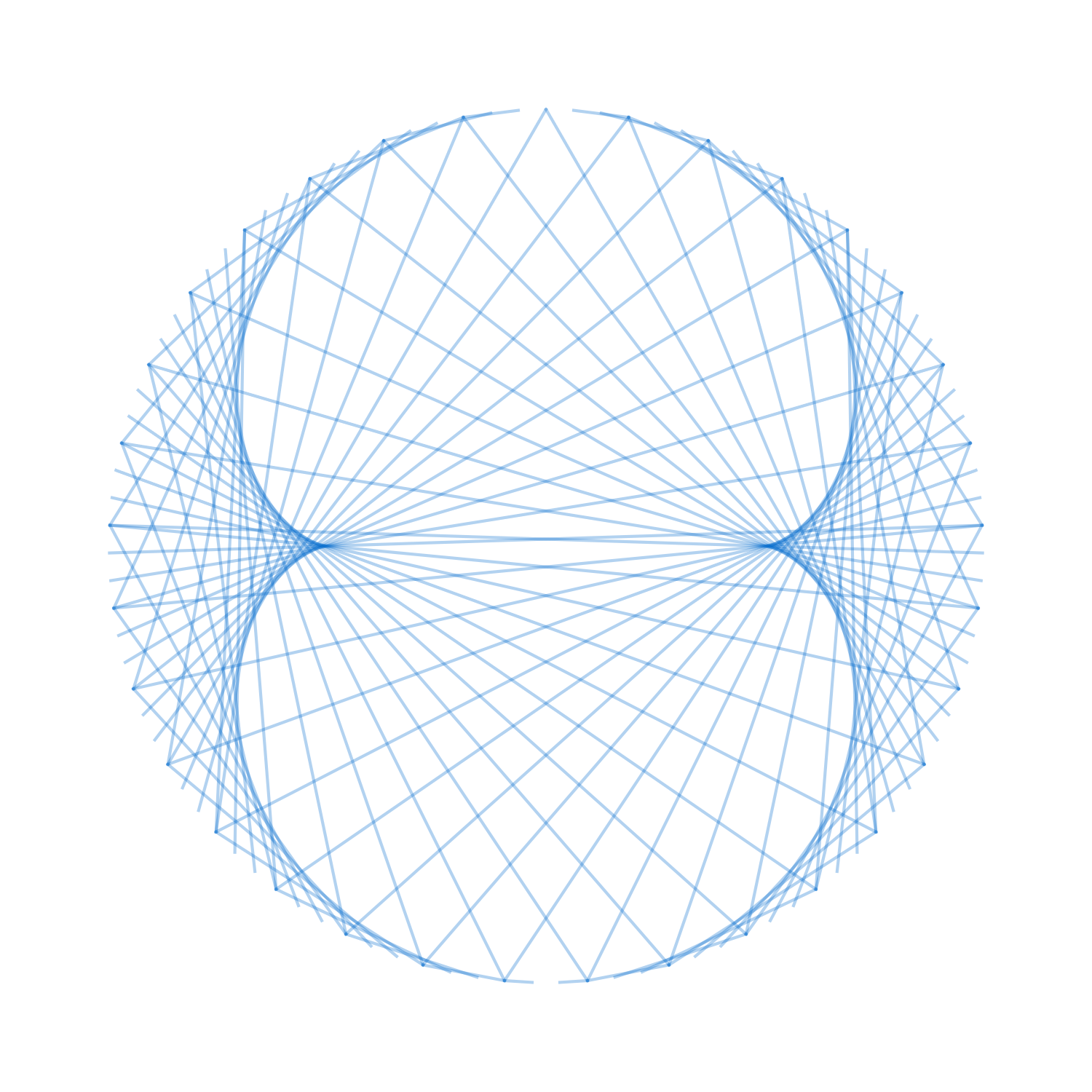
是不是有点眼熟?
当$n=500$时:

已经很明显了:这正是杯子里亮斑的形状。
这只是一个巧合吗?
2 咖啡杯
我们先撇开数学,从物理的角度来考虑杯子里亮斑出现的原因。
首先,亮斑的出现和光的反射有关。入射的光线经过马克杯圆柱形的光滑内壁的反射,照亮了杯底。
但为什么会出现亮斑?亮斑意味着杯底的亮度分布是不均匀的:亮斑要亮一些,其余部分要暗一些。
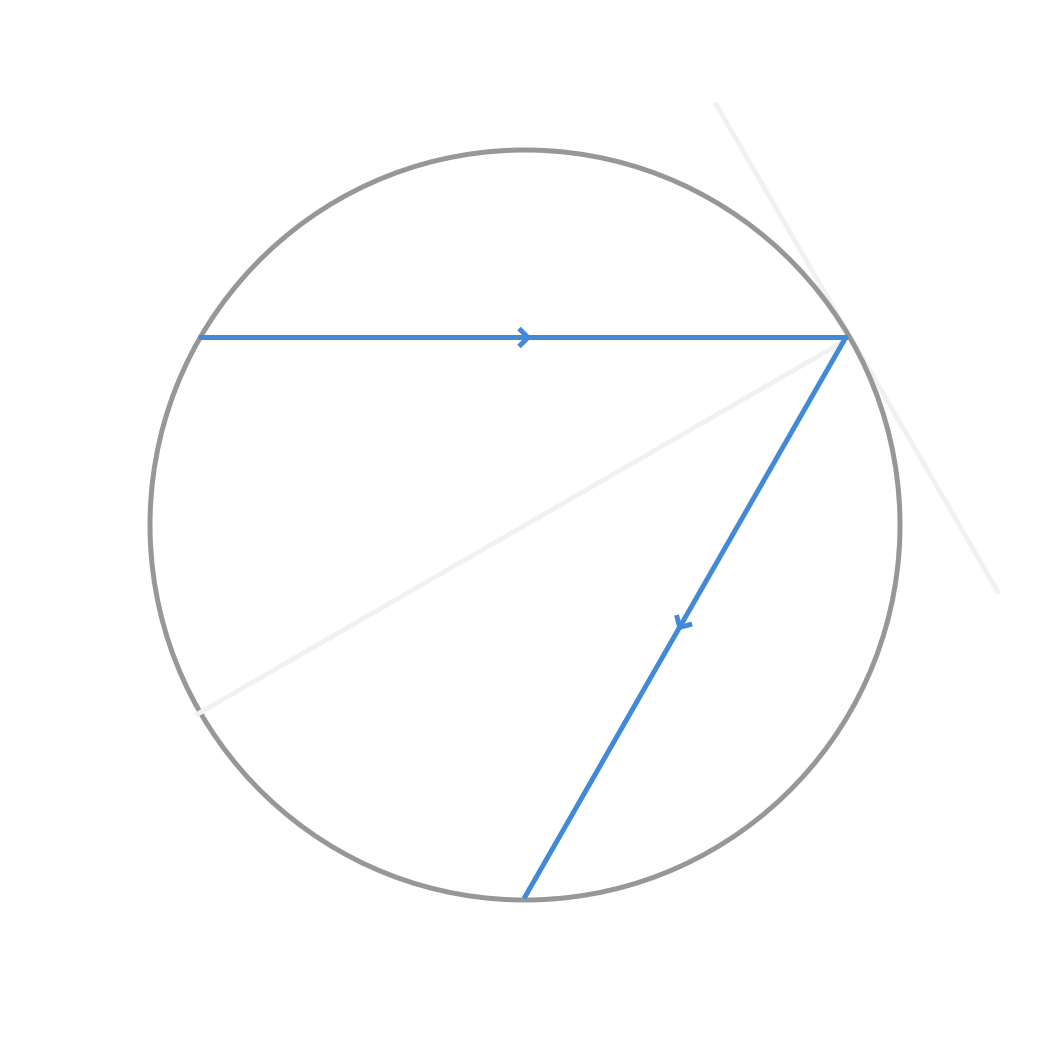
为了简化模型,我们假设入射光是平行光,以及马克杯的内壁是完美的圆柱面。考虑极细的“一条”光线,经过反射之后,它可以照亮底面上的一个点。想象把这条入射光向上平移一些,则反射点会上移,导致底面被照亮的点移动。根据几何关系,在入射光上下平移的过程中,底面上被照亮点的轨迹是一条直线:

因此,我们可以从上往下把整个图形“压扁”,仅考虑其在底面上的投影,将问题简化为二维:
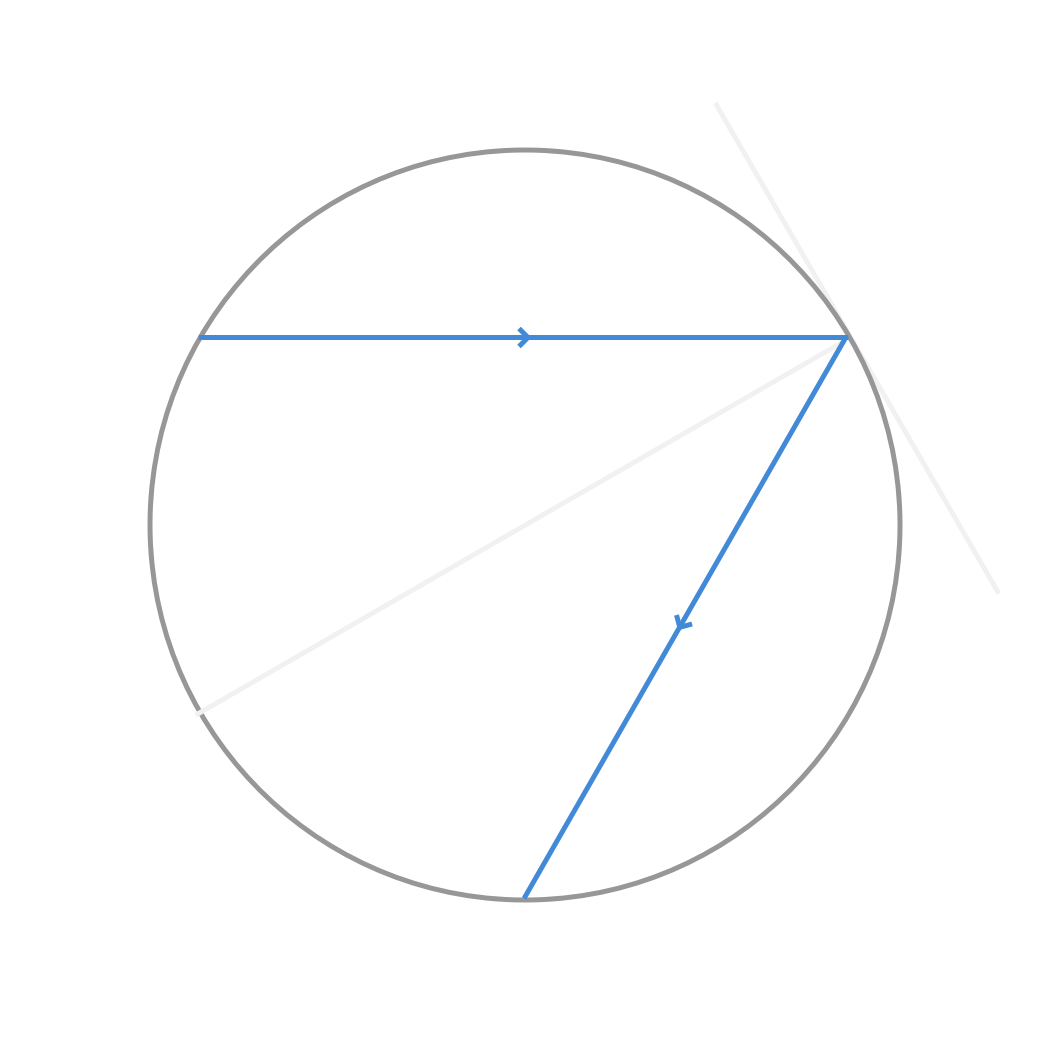
于是,我们只需要考虑一族平行的光线在经过一个圆的反射后,出射光线“构成”的形状。这些出射光线会有一些互相重叠的部分,导致这些部分的亮度更高,也就形成了亮斑。数学上,亮斑的形状就是出射光线这一族曲线的包络线(envelope)。
那这又跟环形乘法表有什么关系呢?

由于圆的对称性,我们只需考虑0位于圆的正上方,入射光水平射入的情况。设入射点对应的数为k。显然0平分了入射光所对的圆弧,且入射光与出射光所对的圆弧长度相等,因此出射光与圆相交的点对应的数是3k。也就是说,从0到3k的弧长正好是0到k的弧长的3倍。这正是此前乘法表中“乘以3”的几何意义!
3 轮子
我们还剩下一个问题:这条曲线究竟是什么曲线?
这里给出一种解法。
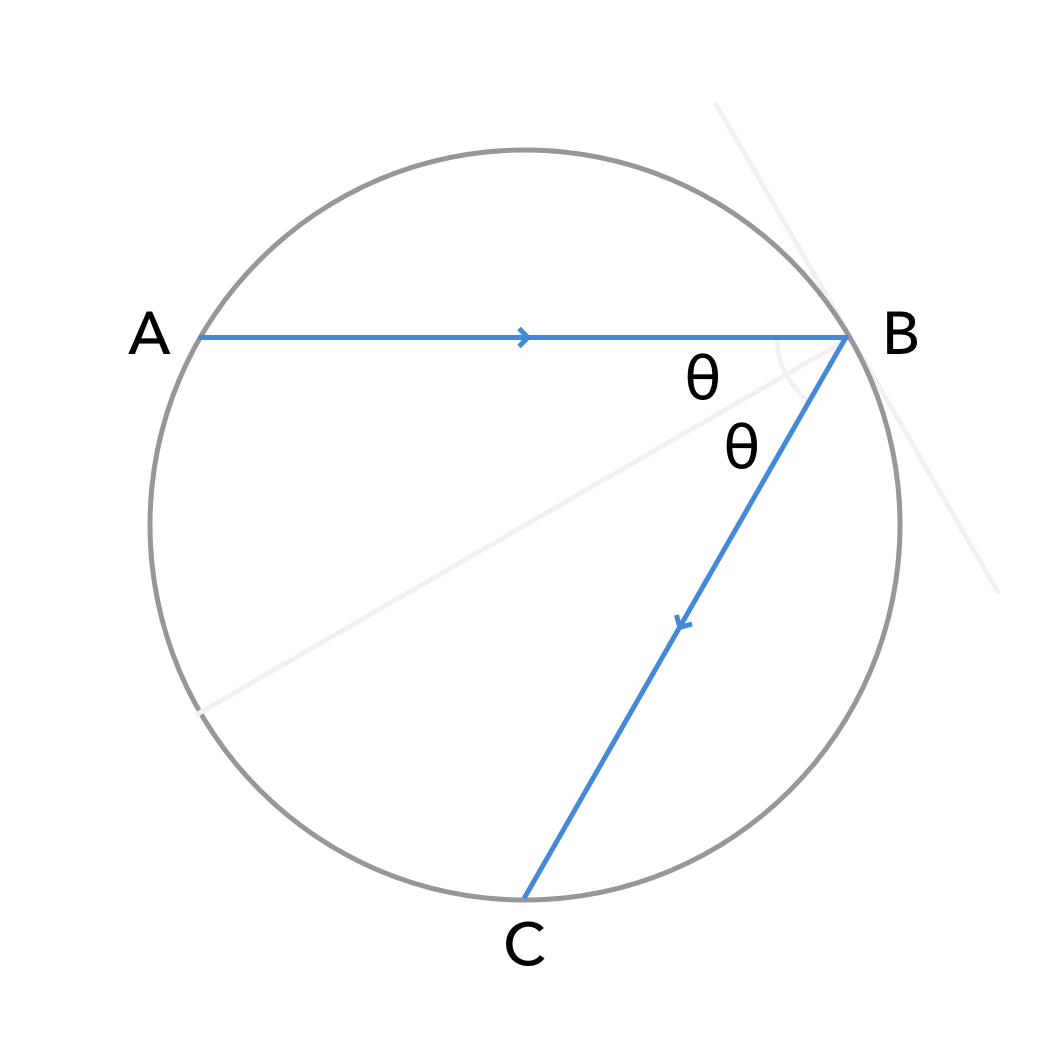
设入射光的方程为$y=t \ (-1\leq t \leq 1)$,圆的方程为$x^2+y^2=1$.
联立方程,解得点B的坐标为$(\sqrt{1-t^2},t)$.
由几何关系,得$\tan{\theta}=\frac{t}{\sqrt{1-t^2}}$.
因此直线BC的斜率为
$$k_{BC} = \tan{2\theta} = \frac{2\tan\theta}{1-\tan^2\theta} = \frac{2t \sqrt{1-t^2}}{1-2t^2}$$
有了B点坐标和BC的斜率,就可以求直线BC的方程了,化简后为
$$ 2t\sqrt{1-t^2}x + (2t^2-1)y-t=0 $$
记
$$ F(x,y,t) = 2t\sqrt{1-t^2}x + (2t^2-1)y-t $$
包络线满足的必要条件有$F(x,y,t)=0$以及$\frac{\partial F(x,y,t)}{\partial t}=0$.
化简后作代换$t=\sin\theta$,再化简得到
$$
\begin{cases}
x \sin{2\theta}-y \cos{2\theta} &=\sin\theta \\
2x \cos{2\theta}+2y \sin{2\theta} &=\cos\theta
\end{cases}
$$
似乎没法消掉$\theta$. 那就留着吧,解出$x$和$y$,化简后就得到了包络线的参数方程
$$
\begin{cases}
x &= \frac{1}{4} (3 \cos \theta -\cos {3 \theta} ) \\
y &= \sin ^3{\theta}
\end{cases}
$$
好像还是不认识。没关系,三角变形一下:
$$
\begin{cases}
x &= \frac{1}{4} (3 \cos \theta -\cos {3 \theta} ) \\
y &= \frac{1}{4} (3 \sin \theta -\sin {3 \theta} )
\end{cases}
$$
终于露出了庐山真面目:这是一条外旋轮线(epicycloid)的参数方程。其中大圆半径为$\frac{1}{2}$,小圆半径为$\frac{1}{4}$,大小圆半径比为2:1.

问题到这里基本就解决了。
4 One more thing
之前在乘法表中,只展示了$m=3$的情况。如果改变$m$的值,包络线又会变成什么形状呢?
更一般地,我们甚至可以推广一下,改变$r$的定义,让$m$可以取任意实数值:
$$ r = \left \lfloor{mk \mod n}\right \rfloor $$
其实就是加了一个向下取整。结果非常的漂亮:

可以看到,乘法表中出现的包络线是大小圆半径比为$m-1:1$的外旋轮线。
特别地,大小圆半径比为2:1的外旋轮线又被称为肾形线(nephroid);而比为1:1的外旋轮线就是著名的心形线(cardioid)。
在光学中,这种一族光线被反射后的包络线也被称为焦散线(caustic)。回想一下圆锥曲线的光学性质,只有抛物线可以将平行光汇聚在一点上,而我们证明了圆是办不到的。
除此之外,通过几何方法也可以证明这是一条外旋轮线。方法在最后一条参考资料[5]中。
参考资料
[1] https://www.youtube.com/watch?v=qhbuKbxJsk8
[2] http://mathworld.wolfram.com/CircleCatacaustic.html
[3] https://en.wikipedia.org/wiki/Epicycloid
[4] https://en.wikipedia.org/wiki/Caustic_(mathematics)
[5] https://sinews.siam.org/Details-Page/focusing-on-nephroids